www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » ›
Tentukan hasil dari \( \int \frac{x}{\sqrt{1-x^2}} \ dx = \cdots \ ? \)
Pembahasan:
Untuk menyelesaikan soal ini kita dapat gunakan teknik integral substitusi trigonometri. Misalkan \(x = \sin t \) sehingga didapatkan hasil sebagai berikut:

Selanjutnya, gunakan hasil di atas untuk menyelesaikan integral dalam soal ini, yaitu:
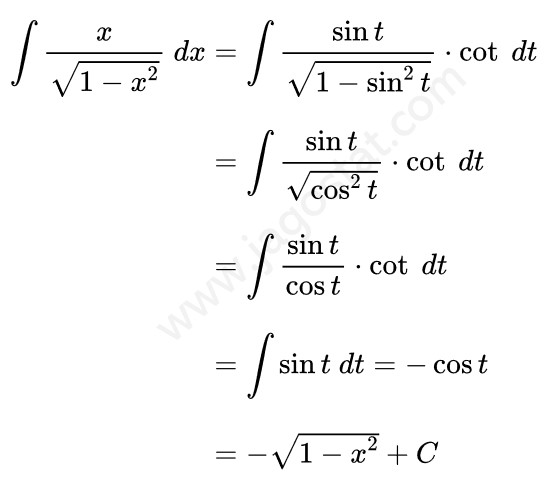
Keterangan:
Untuk mencari nilai \( \cos t \) kita bisa gambarkan segitiga siku-siku berdasarkan pemisalan yang kita buat di awal tadi. Selanjutnya kita cari sisi lain dari segitiga tersebut yang belum diketahui menggunakan rumus Phytagoras. Berikut hasil yang kita peroleh:
